Evolutionary dynamics of dispersal – Lattice models of ecological dynamics (mentor: Dr. Ted Galanthay)
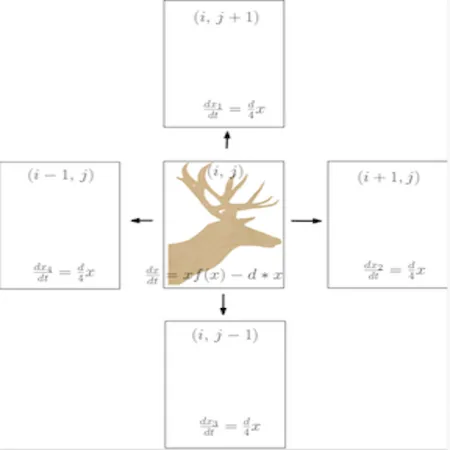
Dispersal is a heritable trait of both plants and animals. The decision of when, where, and how to disperse can be influenced by local environmental information. Dispersal success is affected by the ecological costs that may be incurred by the organism at one or more life stages . Rapid global environmental change and its effects on habitat connectivity have created an urgent need to better understand how dispersal costs at multiple life stages affect the evolution of dispersal. This project explores theoretically how competition and predation impact the evolution of short- and long-range dispersal strategies when developmental and transitional dispersal costs are considered. For example, plants and insects that disperse locally can develop long-distance dispersal mechanisms (e.g., seed plumes or wing dimorphism) to escape environmental stresses or predation.
Research projects under this topic are motivated by several pressing questions:
- Under what ecological conditions is long-distance dispersal predicted to evolve?
- How does the spatial structure of the environment affect these predictions?
- How do different costs (e.g., assessed to fecundity or predation risk) affect these predictions?