REU Project Descriptions

Evolutionary dynamics of dispersal – Lattice models of ecological dynamics (mentor: Dr. Ted Galanthay)

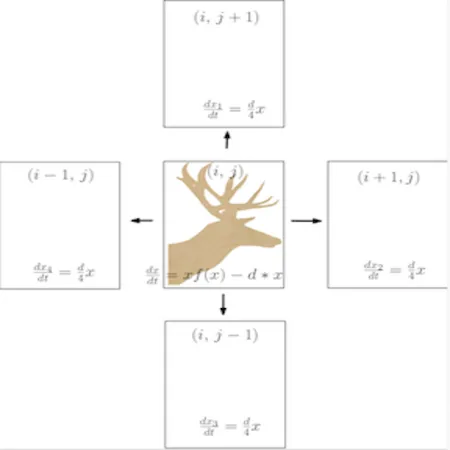
Dispersal is a heritable trait of both plants and animals. The decision of when, where, and how to disperse can be influenced by local environmental information. Dispersal success is affected by the ecological costs that may be incurred by the organism at one or more life stages . Rapid global environmental change and its effects on habitat connectivity have created an urgent need to better understand how dispersal costs at multiple life stages affect the evolution of dispersal. This project explores theoretically how competition and predation impact the evolution of short- and long-range dispersal strategies when developmental and transitional dispersal costs are considered. For example, plants and insects that disperse locally can develop long-distance dispersal mechanisms (e.g., seed plumes or wing dimorphism) to escape environmental stresses or predation.

Research projects under this topic are motivated by several pressing questions:

1. Under what ecological conditions is long-distance dispersal predicted to evolve?
2. How does the spatial structure of the environment affect these predictions?
3. How do different costs (e.g., assessed to fecundity or predation risk) affect these predictions?

Billiard dynamics on surfaces of revolution (mentor: Dr. Dan Visscher)

The dynamics of a two-dimensional billiard system is determined by the shape of its boundary as well as the curvature of the surface it sits on. Two examples of billiard tables in the plane with regular (integrable) dynamics are rectangles and ellipses. While they generate simple dynamics on their own, these shapes can be combined into billiard tables with various types of dynamical behaviors. Combined in one way, they form a “mushroom,” whose resulting system displays both elliptic islands (regular behavior) and a chaotic region. A limiting case of this yields the “Bunimovich stadium,” a classic example of a convex billiard table with completely chaotic behavior. Ellipses and rectangles were combined in yet another way to give a solution to the “illumination problem”: a mirrored room (i.e., billiard table) in which it is impossible to illuminate the entire room from a single light source.

Billiards have also been studied on surfaces of constant curvature. Much less is known, however, about billiards on surfaces of variable curvature. A few recent papers have started to address this setting: considers the tables on surfaces of variable but everywhere positive curvature, and studies the uniform hyperbolicity of billiards on general surfaces. The proposed project explores the behavior of billiard dynamics on surfaces of revolution, a class of surfaces that can exhibit variable curvature (both positive and negative). Studying surfaces of revolution is more tractable than the general case of variable curvature because of the Clairaut integral, a remarkably simple equation that determines the trajectory of geodesics on these surfaces. Because the sphere and pseudosphere are both surfaces of revolution themselves, this is a natural extension of working with billiards on surfaces of constant curvature.

Research projects under this topic can explore multiple questions:

Are analogs of known integrable constant curvature billiards also integrable on variable curvature surfaces of revolution? Are there other examples of integrable billiards on surfaces of revolution?

Are analogs of known chaotic billiards on constant curvature surfaces also chaotic on variable curvature surfaces of revolution? How do their Lyapunov exponents compare?

Are there interesting examples of unilluminable rooms on surfaces of revolution?

Pruned fractal trees – Iterated function systems with memory (mentor: Dr. Dave Brown)

This project explores a variant of iterated function systems (IFS) that describe attractors for fractal trees. In previous work, students determined the critical scaling ratios for planar binary branching trees which, for given branching angles, result in attractors that are connected sets. This project considers what happens when specific compositions of functions are forbidden to be used in building the tree and its associated fractal attractor. This effectively removes particular branches (and the branches that grow off from them) from the tree structure; hence, we call these pruned trees.

Students will explore how the pruning affects the topology of the associated fractal attractor. In many cases, pruning causes the tree to lose connectivity; while in others, this does not occur. Even in cases where connectivity is lost, a rescaling of the pruned IFS sometimes re-establishes connectivity. Some non-pruned trees exhibit fractal attractors that are space filling, and pruning may or may not result in complete loss of this space-filling property. Students will explore the relationships among the pruning sequence, the scaling ratio, and the branching angle as they investigate the topology of the fractal attractors. Students will create visualizations using Python or Sage and apply them to provide visual clues to conjecture about the topology of the attractors. They will then use analysis to move toward proving their conjectures.

These pruned trees are an example of an IFS with memory. IFS with memory has been the focus of recent research and is simply an IFS in which certain compositions of the IFS mappings are forbidden to occur. Students will read the literature regarding IFS with memory to understand the theory behind the pruning sequences and determine ways to apply that theory to their own work. A further goal is to apply pruning to three-dimensional fractal trees to again understand the effects of pruning on the topology of the three-dimensional tree attractors.

Multiple questions can be explored in this project:

1. How does the topological structure of the attractor for a fractal tree change with the introduction of pruning?
2. How does rescaling affect the structure of the attractors of pruned fractal trees?